深度学习python库

numpy

import numpy as np

变量及基本操作

矩阵

list1 = [  
    [1, 2, 3, 4],  
    [5, 6, 7, 8],  
    [9, 10, 11, 12],  
    [13, 14, 15, 16]  
]

array1 = np.array(list1) # 将列表转化为矩阵，打印的效果会不一样

array2 = array1

# 矩阵合并，默认axis = 0, 纵向合并。 axis = 1为横向合并，以此类推
array3 = np.concatenate((array1, array2), axis = 1)

矩阵的切片

print(array3[1:3, 2:4]) # 可以在两个维度进行切片

# 也可以跳着切
list2 = [1, 3]
print(array3[:, list2])

torch

变量及基本操作

张量 tensor

tensor1 = torch.tensor(list1)  
  
print(array1)  
print(tensor1)

输出如下： tensor与array的区别仅在于tensor将array放在了一张张量网上，可以进行梯度计算

梯度计算

x = torch.tensor(3.0)
x.requires_grad_(True)
y = x**2
y.backward() # 2x = 6

# 每个变量的梯度会在变量中进行记录，如果对一个变量分别求两次梯度，需进行清零。否则会出现梯度累加，导致计算错误，如本例中不进行清零x的梯度将为6 + 6 = 12
x.grad = torch.tensor(0.0)
y2 = x**2
y2.backward() #2x = 6

x.detach() # 将x在张量网上摘下，不再计算梯度

创建张量

tensor1 = torch.ones((10,1)) # 创建一个10行1列全是1的张量
tensor0 = torch.zeros((10,1)) # 创建一个10行1列全是0的张量
tensor2 = torch.normal(mean, std, shape) # 创建一个形状为shape，均值为mean，标准差为std的正态分布的张量
# ep
tensor2 = torch.normal(0, 0.01, (3, 10, 4)) # 均值为0，标准差为0.01，形状3维10行4列

张量求和

sum1 = torch.sum(tensor1, dim = 0 or 1, keepdim = True) # 0按列求和，1按行求和; keepdim保持原shape打印

张量形状

tensor.shape

tensor.backward()

在PyTorch中，tensor.backward() 是实现自动微分（Autograd）的核心方法。它的主要作用是计算当前张量相对于某个标量值的梯度，并存储在相应张量的 .grad 属性中。以下是关键要点：

1. 基本用法：

x = torch.tensor(2.0, requires_grad=True)
y = x ** 2
y.backward()  # 计算梯度
print(x.grad)  # 输出：tensor(4.)

2. 工作原理：

• 构建计算图：所有涉及requires_grad=True张量的运算都会记录在动态计算图中
• 反向传播：从调用backward()的张量开始，反向遍历计算图应用链式法则
• 梯度累积：结果梯度会累加到叶子节点的.grad属性中

3. 参数说明：

# 当输出是非标量时需指定梯度权重
x = torch.randn(3, requires_grad=True)
y = x * 2
y.backward(gradient=torch.tensor([1., 1., 1.]))  # 等效于y.sum().backward()

# 保留计算图结构（用于多次反向传播）
loss.backward(retain_graph=True)

4. 典型应用场景：

# 训练循环中的典型用法
for data, target in dataloader:
    optimizer.zero_grad()  # 清空梯度
    output = model(data)
    loss = loss_fn(output, target)
    loss.backward()        # 计算梯度
    optimizer.step()       # 更新参数

注意事项：

• 梯度会自动累积，需手动调用zero_grad()清除
• 默认会释放计算图，二次调用backward()需设置retain_graph=True
• 只能对标量值直接调用backward()，多维张量需提供gradient参数
  以下是关于PyTorch中tensor.backward()两个关键机制的深入解释：

---

1. 默认释放计算图与retain_graph=True的作用

原理

PyTorch的自动微分系统基于动态计算图（Dynamic Computation Graph）。当调用backward()时：

• 默认行为：反向传播完成后，计算图会被立即释放以节省内存。
• 问题：如果尝试再次调用backward()，由于计算图已销毁，会抛出RuntimeError。

示例

x = torch.tensor(2.0, requires_grad=True)
y = x ** 3

# 第一次反向传播（正常执行）
y.backward()  
print(x.grad)  # 输出: tensor(12.)

# 第二次反向传播（会报错）
y.backward()  # ❌ RuntimeError: Trying to backward through the graph a second time

解决方案

通过retain_graph=True保留计算图：

y.backward(retain_graph=True)  # 第一次反向传播保留计算图
y.backward()                   # ✅ 可再次执行
print(x.grad)                  # 梯度累积为 12 + 12 = 24

注意

• 内存开销：保留计算图会增加内存占用，需谨慎使用
• 应用场景：如GAN需要交替训练生成器和判别器时
• 替代方案：使用torch.autograd.grad()直接计算梯度（不修改.grad属性）

---

2. 标量限制与gradient参数的作用

原理

• 标量限制：数学上梯度定义为标量函数对张量的导数。当输出是非标量时，PyTorch无法确定如何聚合多维输出的梯度。
• gradient参数：本质是一个权重向量，用于计算加权和的梯度（相当于torch.sum(gradient * output)）。

示例

x = torch.tensor([1.0, 2.0], requires_grad=True)
y = x * 2  # y = [2.0, 4.0]

# ❌ 直接调用会报错
y.backward()  # RuntimeError: grad can be implicitly created only for scalar outputs

# ✅ 正确方式：提供gradient参数
y.backward(gradient=torch.tensor([1., 1.]))  
print(x.grad)  # 输出: tensor([2., 2.]) 
               # 计算过程：d(sum(y))/dx = d(2x1 + 2x2)/dx = [2, 2]

数学等价性

# 以下两种写法等价
y.backward(gradient=torch.tensor([1., 1.]))
# 等价于
y.sum().backward()

高级用法

# 自定义权重计算梯度
gradient_weights = torch.tensor([0.5, 2.0])
y.backward(gradient=gradient_weights)
print(x.grad)  # 输出: tensor([1., 4.]) 
               # 计算：0.5*2 + 2.0*2 = [1, 4]

注意

• 默认行为：当输出是标量时，等价于gradient=torch.tensor(1.0)
• 广播机制：gradient的形状必须与输出张量形状匹配
• 物理意义：可理解为对多维输出不同通道的梯度重要性加权

梯度计算解牛

1. 梯度计算的本质

PyTorch的梯度计算本质上是 逐元素（element-wise） 进行的。对于任意形状的张量：

• 梯度张量与原张量形状 严格一致
• 每个元素的梯度表示 该元素对最终标量损失值的贡献

示例代码中的 w_0

true_w = torch.tensor([10.0, 7.0, 5.0, 2.0])  # 4维向量
w_0 = torch.normal(0, 0.01, true_w.shape, requires_grad=True)  # 形状为 (4,)

当调用 loss.backward() 时：

• 系统会计算损失值对 w_0 的 每个元素 的偏导数
• 最终 w_0.grad 也会是一个形状为 (4,) 的张量

---

2. 计算过程可视化

假设当前 w_0 和梯度如下：

w_0 = tensor([w1, w2, w3, w4], requires_grad=True)  # 实际值可能是 [0.1, -0.2, 0.05, 0.3]
grad = tensor([dw1, dw2, dw3, dw4])                # 例如 [1.2, 0.8, -0.5, 2.1]

参数更新操作：

w_0 -= lr * w_0.grad
# 等价于：
w1_new = w1 - lr * dw1
w2_new = w2 - lr * dw2
w3_new = w3 - lr * dw3
w4_new = w4 - lr * dw4

---

3. 数学推导验证

---

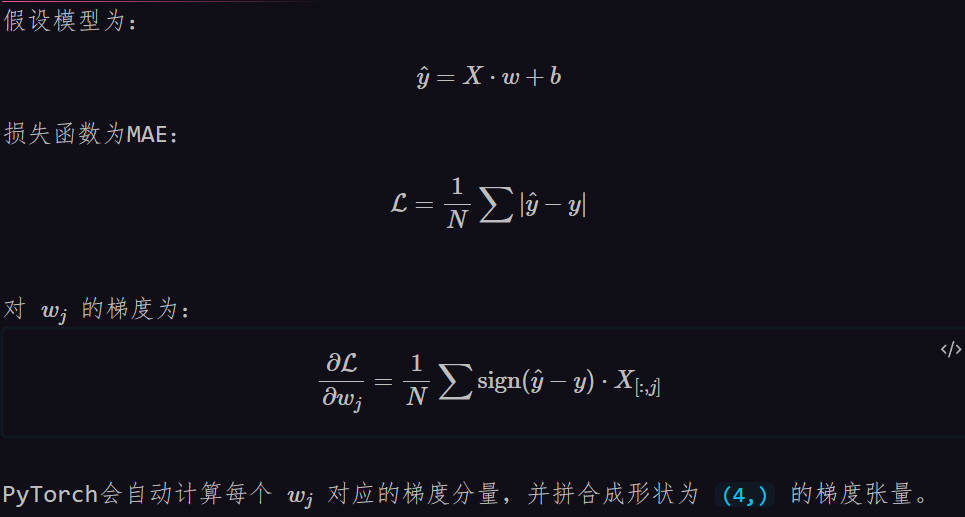
4. 代码执行细节验证

在你的代码中：

def fun(x, w, b):
    pred_y = torch.matmul(x, w) + b  # x形状(batch_size,4), w形状(4,)
    return pred_y                    # 输出形状(batch_size,)

def maeLoss(pred_y, y):
    return torch.sum(abs(pred_y-y))/len(y)  # 输出是标量

反向传播时：

1. loss 是标量（关键！）
2. 通过链式法则，PyTorch会自动计算标量损失对每个 w_j 的梯度
3. 所有梯度按原始维度组织，存储在 w_0.grad

---

5. 梯度形状验证实验

可以添加调试代码验证梯度形状：

print(w_0.shape)        # 输出: torch.Size([4])
print(w_0.grad.shape)   # 反向传播后会输出: torch.Size([4])

---

6. 与一维情况的对比

参数类型	参数形状	梯度形状	更新方式
标量	()	()	w -= lr * w.grad
向量	(4,)	(4,)	逐元素更新
矩阵	(3,4)	(3,4)	每个矩阵元素独立更新

---

为什么没有维度冲突？

• 关键点：损失函数最终输出始终是 标量（maeLoss 返回的是平均值）
• 数学保证：标量对任意维度张量的导数自然保持与原张量相同的形状
• PyTorch特性：自动微分系统会处理任意维度的张量梯度计算

---

常见误区澄清

误区：“多维张量需要特殊处理才能计算梯度”

事实：

• 只要最终损失是标量，PyTorch可以处理任意维度的参数梯度
• 无论参数是标量、向量、矩阵还是高阶张量，梯度计算规则一致
• 参数更新时的逐元素操作是自动完成的

matplotlib.pyplot

plt.plot()

在使用 PyTorch 进行深度学习训练时，如果要将张量数据传递给 matplotlib.pyplot.plot() 进行可视化，通常需要添加 .detach().numpy() 操作。这是由 PyTorch 张量和 Matplotlib 的底层机制差异导致的，具体原因如下：

---

1. 核心原因：数据格式转换

操作步骤	作用	必要性
.detach()	将张量从计算图中分离，得到一个不需要梯度追踪的新张量	必要
.numpy()	将 PyTorch 张量转换为 NumPy 数组（Matplotlib 只能处理 NumPy 数组或 Python 原生数据类型）	必要

---

2. 分步详解

（1）脱离计算图（.detach()）

• 问题背景：PyTorch 张量可能带有梯度信息（requires_grad=True）
• 风险：如果直接使用带有梯度的张量：
  • 会增加不必要的内存占用（保持计算图）
  • 可能引发意外的梯度传播（尽管绘图操作不需要梯度）
• 示例对比：

  # 原始张量（带梯度）
  tensor_with_grad = torch.tensor([1.0, 2.0], requires_grad=True)
  
  # 直接转换会报错
  try:
      plt.plot(tensor_with_grad)  # ❌ 报错：Can't call numpy() on Tensor that requires grad
  except Exception as e:
      print(e)
  
  # 正确做法
  plt.plot(tensor_with_grad.detach().numpy())  # ✅ 正常工作

（2）设备转移（CPU/GPU）

• 问题背景：如果张量在 GPU 上（device='cuda'）
• 风险：Matplotlib 无法直接处理 GPU 上的张量
• 完整转换流程：

  # GPU 张量处理流程
  gpu_tensor = torch.tensor([1.0, 2.0], device='cuda')
  
  # 错误方式
  plt.plot(gpu_tensor.cpu().detach().numpy())  # ❌ 顺序错误，应先 detach
  
  # 正确方式
  plt.plot(gpu_tensor.detach().cpu().numpy())  # ✅ 正确顺序：detach → cpu → numpy

（3）数据类型转换

数据类型	说明
PyTorch Tensor	可以是任意形状和数据类型（float32, int64 等）
NumPy Array	Matplotlib 的底层数据容器，与 PyTorch 内存不兼容

---

3. 完整转换流程

# 假设有一个需要绘制的 PyTorch 张量
original_tensor = torch.randn(100, requires_grad=True, device='cuda')

# 安全转换步骤
plot_data = original_tensor.detach()  # 1. 脱离计算图
                .cpu()                # 2. 转移到 CPU（如果是 GPU 张量）
                .numpy()              # 3. 转换为 NumPy 数组

# 绘制图形
plt.plot(plot_data)
plt.show()

---

4. 常见错误场景

场景 1：未分离计算图

x = torch.linspace(0, 2*np.pi, 100, requires_grad=True)
y = torch.sin(x)

plt.plot(x.numpy(), y.numpy())  # ❌ RuntimeError: Can't call numpy() on Tensor that requires grad

场景 2：未处理 GPU 张量

gpu_data = torch.randn(10).cuda()
plt.plot(gpu_data.detach().numpy())  # ❌ TypeError: can't convert cuda:0 device type tensor to numpy

场景 3：错误操作顺序

# 先转 NumPy 再 detach 会丢失梯度信息
temp = y.numpy()         # ❌ 错误开始点
detached = temp.detach() # ❌ AttributeError: 'numpy.ndarray' object has no attribute 'detach'

---

5. 最佳实践总结

操作类型	推荐写法	说明
CPU + 无梯度	tensor.numpy()	直接转换
CPU + 有梯度	tensor.detach().numpy()	必须 detach
GPU + 无梯度	tensor.cpu().numpy()	需要转移到 CPU
GPU + 有梯度	tensor.detach().cpu().numpy()	完整流程

---

6. 特殊场景处理

保留梯度但需要可视化

如果需要在可视化后继续梯度计算（罕见需求）：

# 使用 with torch.no_grad(): 临时禁用梯度
with torch.no_grad():
    plt.plot(x.cpu().numpy(), y.cpu().numpy())

批量处理张量

对于高维张量（如神经网络中间层输出）：

# 假设 feature_map 是 4D 张量 (batch, channel, height, width)
feature_map = model(inputs)
plt.imshow(feature_map[0, 0].detach().cpu().numpy())  # 可视化第一个样本的第一个通道

---

总结

.detach().numpy()（对于 GPU 张量还需 .cpu()）的组合操作是 PyTorch 与 Matplotlib 协作的 必要桥梁，其主要作用包括：

1. 断开梯度传播：防止可视化操作影响反向传播
2. 设备转移：确保数据位于 CPU 内存
3. 格式转换：将张量转换为 Matplotlib 可识别的 NumPy 数组

这种转换虽然增加了代码的复杂度，但能有效避免许多隐蔽的错误，是 PyTorch 可视化过程中必须掌握的关键技巧。